Matematik çalışırken kaleme dokunma, sadece biraz düşün!

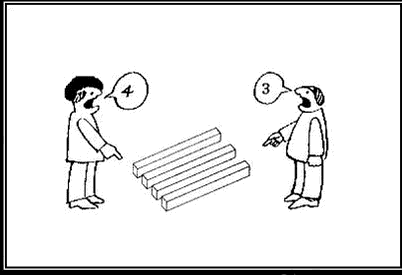
Lisede gösterilen temel matematik için bile denir ya “bu öğrendiklerimizi ileride kullanmayacağız ki”, işte yanlış eğitim öğrencilerde yanlış yaklaşımı doğuruyor. Matematik her yerde, hemen her alanda kullanılıyor. Sadece neyi nerede kullanacağını bilmen ve anlaman lazım. Bazı öğrenciler tamamen ezbere dayalı öğreniyor çoğu şeyi. Mesela havuz problemleriyle alakalı 2-3 soru çeşidini görüyor, nasıl çözüleceğini ezberliyor. Sınavda aynı konuyla ilgili farklı tip soru çıkınca kalem oynatamıyor, çünkü ilk defa sınav esnasında düşünmeye başlıyor konu hakkında. Bu anlamda matematik insanı çok kolay ters köşe yapar ama zamanla haşır neşir oldukça farklı bakış açıları öğretir.

Örneğin tek bir sorunun onlarca değişik çözümü olabiliyor. Bir yerden başladık ve sıkıştıysak, bazen başa dönüp başka bir yerden bakmak çok işe yarıyor. Mesela, aşağıdaki eşitlikleri kanıtlarken cebirsel işlemler ilk akla gelen yol olsa da kombinatorik ispatları daha güzel aslında.

İlk örnek olarak 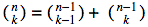 özdeşliğini göstermemiz istendiğinde, genelde eşitliği

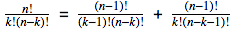 olarak yazıp, birkaç işlemden sonra sonuca ulaşırız.

(NOT: 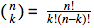 = n elemanlı bir kümenin r’lı kombinasyonlarının sayısı)

Halbuki, bu özdeşliği ispatlamanın çok daha akıllıca bir yolu var. Şimdi n kişilik bir topluluk düşünelim ve bu n kişiden biri özel olsun. Bu özel kişiye İkbal diyelim. Özdeşliğin sağ tarafı bu n kişiden k tanesini kaç değişik şekilde seçebileceğimizi veriyor. Olaya İkbal açısından baktığımızda k kişiyi seçebileceğimiz yalnızca iki durum var; 

İkbal’in bu k kişi arasında seçilmesi ya da seçilmemesi. İkbal’i seçtiğimiz durumda, geriye kalan n-1 kişiden k-1 kişiye ihtiyacımız var; 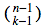. İkbal’in seçilmediği durumda ise geriye kalan n-1 kişiden k tanesini ayırmak gerekiyor; 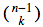. Yani n kişiden k tanesini  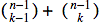farklı şekilde seçebiliriz ki bu da özdeşliğin sol tarafını verir.

Benim sevdiğim yöntemlerden biri olduğu için yine benzer ispatlardan ama bir tık zor bir teoremin ispatıyla devam edeceğim.

Multinomial Teorem der ki;

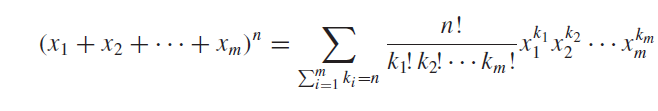
(Burada k_i'ler negatif olmayan tam sayılar)

İSPATI:

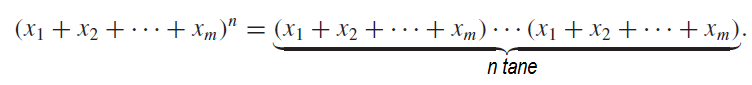
Bu açılımda üstteki eşitliğin x₁^k₁  x₂^k₂ …x_m^k_m  terimini elde etmek için n tane çarpanımızın k₁ tanesinden x₁, kalan n-k₁ çarpanın k₂ tanesinden x₂,… ve son olarak da geriye kalan n-k₁-k₂-…-k_m-1 çarpanın k_m tanesinden x_m çarpanı gelmesi gerekiyor. Bu da n’in m tane negatif olmayan tam sayıya dağıtılmasına tekabül ediyor. ( k₁+k₂+…+ k_m= n )

Farklı dağılımların sayısı 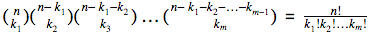 olarak bulunur. Böylelikle elde ettiğimiz sonuç teoremi ispatlıyor. Kabul ediyorum bunu düşünebilmek biraz matematikle ilgili olmayı gerektiriyor ama şimdi sorsam x²+ y²=z² eşitliğini sağlayan sonsuz sayıda x, y, z tam sayı üçlüsü olduğunu gösterin diye, bir kısmınız eline kağıt, kalem alıp uğraşmaya başlar. Aslında hiç işlem yapmadan ortaokul geometri bilgisi yetiyor. Dik üçgenlerde Pisagor Teoremi’ni ve 3-4-5 özel üçgenini eminim çoğumuz biliyoruz. Eğer x=3k, y=4k alırsak k’nın tüm pozitif tam sayı değerleri bize sonsuz tane çözüm verir. Kalem oynatmadan düşünülebilir bir şey yani.

En baştaki matematiğe ilgili olmayan bir kısım öğrencinin meşhur “bunları nerede kullanacağız” sorusuna gelirsek, burada uzun uzadıya tüm meslek gruplarını inceleyemem ama şu çok net ki matematik eğitimi her meslek grubundaki insana perspektif kazandırıp, zihnini geliştirir. Tabi kaleme dokunmadan önce düşünmeyi öğrenebilirsek.

Kaynaklar
1- Ross, Sheldon (2009). A First Course In Probability (8th Edition). Prentice Hall.
2- The American Mathematical Monthly, Vol. 123, No. 1 (January 2016), pp. 94-96

Görsel Kaynaklar
http://xahlee.info/math/i/point_of_views.png
http://www.branfordseven.com/education/what-is-the-algorithm/article_bc6bd178-47b6-11e3-baf5-001a4bcf6878.html

Kapak Görseli
Shuttterstock