Franck-Hertz Deneyi Nedir?

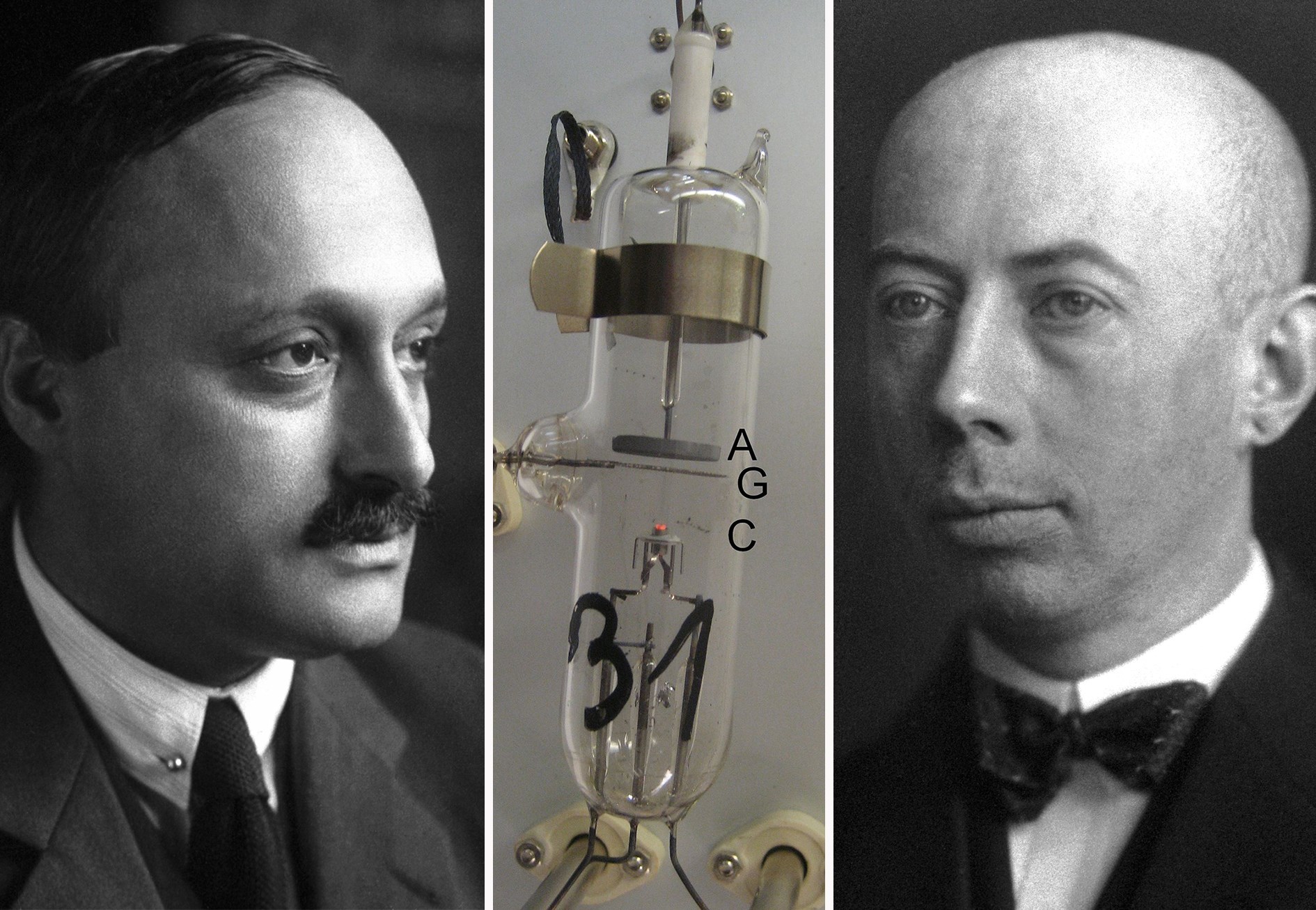
Bohr atom modeline göre, bir atomdaki elektronlar çekirdek etrafında belirli enerji seviyelerinde hareket ederler. Elektronların enerjilerini arttırarak, temel durumda bulunan elektronu daha üst enerji seviyelerine çıkarmak için yeterli enerjiye uyarma, atomdan uzaklaştırmak için gerekli enerjiye ise iyonlaşma enerjisi denir. Atomların ışıma spektrumunu oluşturan çizgiler, aralıklı enerji düzeylerinin bir kanıtıdır.

Atomların enerji düzeylerinin kesikliliğini kanıtlayan ilk deney Franck-Hertz deneyidir. J. Franck ve G.L. Hertz 1914 yılında yaptıkları deney ile elektronların kesikli enerji seviyelerinde olduklarını kanıtladır.

Deneyde, Franck-Hertz tüpü içerisindeki sıvı cüva buharlaştırılarak, civa atomları serbest elektronlar ile çarpıştırılarak civa atomlarının uyarılması sağlanır. Deney düzeneğinde tüpün bir ucunda, ısıtıldığında elektron saçan bir katot, diğer ucunda da yüzeyine ulaşan elektronları toplayarak akım oluşturan bir anot bulunmaktadır. Bu ikisinin arasına ayrıca, elektronları hızlandırmak için, katoda belirli bir uzaklıkta ızgara yerleştirilmiştir. Katotla ızgara arasına bir V hızlandırma gerilimi uygulanır. Dolayısıyla arasında yaklaşık olarak sabit bir elektrik alan vardır.

Hızlandırıcı gerilim uygulanan elektronların kinetik enerjisi artar ve bu elektronlar civa atomları ile çarpışırlar. Bu çarpışmalar esnek ve esnek olmayan çarpışmalar olmak üzere iki çeşittir.

Izgara ve anot arasına ise durdurucu gerilim uygulanır. Bu durdurucu gerilim, civa atomları ile çarpışan elektronların hangilerinin anota ulaşacağını belirler. Hızlandırıcı gerilimin düşük değerlerinde elektronlar çok az bir kinetik enerji kazanırlar. Bu durumda elektronların kinetik enerjileri civa atomunun uyarılma enerjilerinden düşüktür ve elektronlar civa atomları ile sadece esnek çarpışma yaparlar.

Saf esnek çarpışmalarda sistemin toplam kinetik enerjisi değişmez. Civa atomları ile çarpışan elektronlar kinetik enerjilerini korudukları için durdurucu gerilimi aşarak anota ulaşırlar. Böylelikle anot akımı artar. Hızlandırıcı gerilim arttırılmaya devam ettiğinde daha çok elektron anota ulaşacak ve akım artmaya devam edecektir.

Hızlanan elektron kinetik enerjisi civanın uyarılma enerjisine eşit olduğunda bu çarpışmada esnek olmayan çarpışma meydana gelir. (Civa atomu için uyarılma enerjisi 4.9V’dur) Bunun sonucunda serbest elektronun kinetik enerjisi civa atomundaki bir elektronun enerjisini yükselterek civa atomunun uyarılmasını sağlar. Bu yolla, kazandığı tüm kinetik enerjiyi kaybeden elektron durdurucu gerilimi aşamaz ve anota ulaşamaz. Böylece ani bir düşüş meydana gelir.

Hızlandırma gerilimi bu değerden sonra tekrar arttırıldığında akim yine artmaya başlar. Tam iki katı olduğunda (9.8V), her bir elektron iki tane esnek olmayan çarpışma yaparak iki civa atomunu uyarır. Bu yolla kinetik enerjisini kaybeder, durdurucu gerilimi aşamaz ve akımda tekrar ani bir düşüş meydana gelir. Hızlandırıcı gerilim, uyarılma potansiyelinin her bir tam katına eşit olduğunda bu süreç devam eder. Her seferinde elektron esnek olmayan çarpışmada yer alır.

Anot akımının hızlandırıcı gerilime göre değişimi incelendiğinde [4]’deki gibi bir grafik elde edilir. Bu grafik civa atomu için Franck - Hertz eğrisi olarak adlandırılır. Bu eğride iki tepe arasındaki mesafe eşittir ve bu iki tepe arasındaki potansiyel fark bize civa atomunun uyarılma potansiyelini verecektir.

Uyarılan civa atomları daha sonra bir foton yayarak temel hale geri dönerler. Bu sayede Franck – Hertz deneyi Bohr’un kuantum modelini doğrular. Bu çalışmalarıyla, “bir elektronun atomla çarpışmasını yöneten yasaları keşfetmiş” olduklarından dolayı 1925 Nobel Fizik Ödülü’ne layık görülmüşlerdir.

 

KAYNAKÇA

1. SDÜ Fen-Edebiyat Fakültesi, Kuantum Fiziği Laboratuvarı Deney Föyü, 2011 Isparta, Franck – Hertz Deneyi, syf.-10   Erişim Tarihi: 06.10.2024
2. https://www.youtube.com/watch?v=86I3tVw8Ads&t Erişim Tarihi: 06.10.2024
3. https://www.3bscientific.com/tr/kaide-uezerinde-neon-dolgulu-franck-hertz-tuepue-1000912-u8482230-3b-scientific-teltron,p_1003_2015.html       Erişim Tarihi: 16.10.2024
4. https://www.gtu.edu.tr/Files/UserFiles/90/MF4-FRANCK-HERTZ.pdf ,syf.2 şekil4.2 Erişim Tarihi: 16.10.2024