Jogo Bonito

Ortaokuldayım. Ders müzik, sözlü sınav blok flütten. Notaların inci gibi yazılı olduğu müzik defterimi açıyorum ve onlara bakar gibi yaparak istenilen şarkıyı çalıyorum. “Aferin oğlum, notun dokuz.” Kan ter içerisinde yerime oturuyor ve içimden bir oh çekiyorum. Çok şükür bunu da atlattık. Akşam eve gelince iyi not aldığımı söylüyorum, annem ve babam da haftasonu beraberce maruz kaldığımız işkencenin sonunda bir halta yaradığını öğrenip rahatlıyorlar. Komşularımıza acıyorum. Parmakları delikleri doğru dürüst kapatamayan bir çocuğun kulak tırmalayarak gıcırdattığı bir parçayı saatlerce tekrar tekrar dinlemiş olmanın onlara bu kadarcık bile faydası yok. Bıkkınlık ve sinirle kinlenip flüte deli deli üflemelerimden çektiklerini hiç saymıyorum.

Nefret ediyorum müzik dersinden, nefret, nefret! Aylarca çalıştığım halde nota okuyamıyorum; o yüzden önce notaların isimlerini kurşun kalemle üstlerine not düşüyorum, sonra her bir notayı basmak için parmaklarım sıralarını ezberleyinceye kadar parçayı yüzlerce kez tekrarlıyorum, en son notaların isimlerini siliyorum ki nota okuyamadığım anlaşılmasın. İğrenç bir şey. Sonra da kalkıp sözlüde çalıyorum, yok yani şarkıyı değil, bestekarın kemiklerini sızlatarak şarkının ruhunu (bir hırsız gibi) çalıyorum.

“Bu müzik denilen sanat var ya, çok sıkıcı, çok iğrenç, sadece ezber, keyifsiz bir şey,” dermişim. Yo, yo, bir dakika, hiç de değil. Sadece dersiyle alıp veremediğim. Hatta müziği çok sevdiğim için dersinin böyle olmasına ayrı bir içerliyorum. Öyle böyle değil! Blok flütü dersten sonraki yirmi küsür yıl boyunca gerçek bir enstrüman olarak göremeyecek kadar derin bir yara açılmış içimde. Gene de, sistemin beni müziğin “ne olduğu” konusundaki tüm eğitme çabalarına inat, müzikten nefret etmiyorum, hatta müziği onsuz bir hayat düşünemeyecek kadar seviyorum. Rezil detone sesimle (kimseler yokken) şarkılara kareoke yapacak kadar, radyoda duyduğum bir şarkıyla arabadan inip salsa yapacak kadar, düğün derneklerde millet ne der diye düşünmeden göbek atacak kadar seviyorum.

İşte bu yüzden kendimi çok şanslı hissediyorum. Müzik derslerinin öğrencilerin büyük çoğunluğunu ezberciliğe iten şekli müziğin güzelliğini fark etmeme engel olamadığı için. Çevremdeki insanların büyük çoğunluğu benim kadar şanslı olamayabiliyorlar. Fizik veya matematik derslerinin aynı şekilde, içindeki güzelliği paylaşmadan ezberci şekilde uygulanması sebebiyle fizikten, matematikten korkar, nefret eder oluyorlar. Ders dışında da müzikle tanışmış olduğumuz için müzik dersine olan hıncımızı gerçek müzikle karıştırmıyoruz. Ancak gündelik hayatta fizikle, matematikle yeterince karşılaşmadığımız için bu konuların derslerini gerçek fizikle, gerçek matematikle karıştırıyoruz.

Fizik nere, müzik nere, dediğinizi duyar gibiyim. Bir an için okul yıllarınızdaki fizik derslerinizdeki kızgınlığınızı, kininizi, huzursuzluğunuzu bir kenara koymaya çalışın. Ve uzunca yıllardır dinlemediğiniz ama çok sevdiğiniz bir şarkının radyoda sürpriz bir şekilde karşınıza çıktığını hayal edin. Veya uzunca bir parçanın ortasında aniden gelen ve adeta ruhunuzu yıkayan bir gitar solosunu ilk kez duyduğunuz anda tüylerinizin nasıl diken diken olduğunu hatırlayın. Öyle bir durumda hissettiğiniz saf güzellik hissi nasılsa, bir fizikçinin veya matematikçinin yeni bir şeyler öğrendiği zaman hissettikleri inanın aynı.

Modern tıp da buna yönelik veriler sunuyor bize. Örneğin 2014’de yapılan bir araştırmada 15 matematikçinin beyni 60 farklı formüle bakarken fMRI ile görüntülendi.  Matematikçiler gördükleri formülleri güzel-çirkin diye puanladılar. Sonuçlar gösterdi ki güzel formüller hakikaten mediyal orbito-frontal korteksin A1 alanında aktivite yaratıyorlar, yani beynin görsel sanatlardaki veya müzikteki güzellik ile uyarılan merkezinde.

1+e^(iπ)=0, yani Euler eşitliği, o 60 formül arasındaki güzellik yarışmasının kraliçesi. Gerçekten öylesine muhteşem ki! Eksi sayıların karekökü, dairenin çevresinin çapına oranı, bileşik faizlerin sonsuz küçüklükteki sonsuz vadede toplam ne kadar kazanç sağlayacağı ve yok-var ile eşleştirebileceğimiz sıfır ve bir. Bu birbiriyle tamamen alakasız görünen beş temel matematiksel sabiti, üç temel matematiksel işlem ile ve hepsini sadece birer kere kullanarak birbirine bağlıyor. Sanki sadece suşinin yosununu, dönerin etini, acı halapenyo biberini, fındık ezmesini ve tatlı-ekşi sosu karıştırarak bir yemek yapmışlar ve mucizevi bir şekilde enfes bir tat ortaya çıkmış. Bunu yapan aşçıbaşı sanatkar değilse, nedir?

Euler eşitliğindeki tüm güzelliği görebilmek için biraz yorulmak, hiç olmazsa terimlerin neler olduklarını anlayabilecek kadar çalışıp okumak gerekiyor. Bu da son derece doğal, değil mi? Dünyadaki insanların belki de yarısının ilgi duyduğu alanlarda dahi biraz çalışmadan, öğrenmeden keyif alınamıyor. Jogo Bonito, yani Portekizce “güzel oyun”, tüm zamanların en büyük futbolcularından Pele’nin futbolu tanımlamak için kullandığı terim. Futbolu gençliğinde oynamış, topu kontrol etmenin ve hareket halindeyken nereden nasıl uçacağını takip edebilmenin veya karşındaki rakip oyuncuları ve kaleciyi alt edebilmenin, ne kadar da incelik isteyebileceğini, yani içindeki zanaati bilen birisi Pele’nin oyunundaki güzelliği görebilirken, bunları yapmamış bir çoğumuz için de futbol yirmi küsür kişinin boş boş koşuşturmacası diye görünebiliyor.

Ama Euler eşitliği için şimdilik uğraşmayalım derseniz, yarışmada yüksek puan alan başka güzellere yönelebiliriz: örneğin çoğumuzun pek yakından tanıdığı Pisagor teoremi. Bir dik üçgenin kenar uzunlukları arasındaki bu basit ilişki, bize ortaokul yıllarından beri ezberletilir, ancak nasıl da keşfedildiğinden hiç söz edilmez. Bir sayının karesini almanın, gerçekten bir kare çizip onun alanını ölçmek olarak yorumlanabileceği anlatılırsa, bir tangram oyunu oynarmışçasına yapılabilir bu teoremin kanıtlanması. Çoğu biliminsanı ve matematikçi için gerçek işleri zaten bulmaca çözmek, oyun oynamaktır. Yaratıcı kısmı olmayan fizik, matematik gerçek işin sahte ve ucube bir kopyasıdır.

Pisagor teoremini siz de kanıtlamaya çalışabilirsiniz. 1940’da basılmış bir kitapta 371 farklı ispat yöntemi listelenmiş; bunların bir kısmı cebirsel, bir kısmı geometrik, bir kısmı mühendisvari (yani mekanik aletler yardımıyla), bir kısmı vektör aritmetiği ile. Aralarında Amerika Birleşik Devletleri’nin 12. Başkanı James Garfield’ın 1876’da kongredeki senatörlerle tartışırken bulduğu ispat da var, 16 yaşında bir kız çocuğunun 1938’de yaptığı ispat da.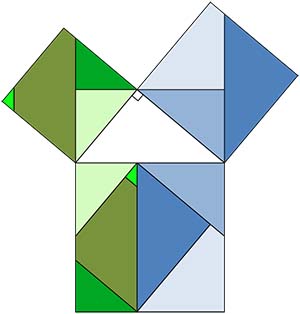

Pisagor teoreminin insanlık tarihinde oynadığı rolü anlatmaya kalksak öyle çok mühendislik uygulaması buluruz ki,  bu yazı rahatlıkla bir kitaba dönüşebilir. Ama kanımca buradaki asıl hikaye teoremin güzelliğinin onu farketme sanşı tanımış insanları nasıl da değiştirebildiğidir. Thomas Hobbes Öklid’in Öğeler serisinin birinci kitabının 47. maddesiyle şans eseri karşılaştığında 40 yaşında bir beşeri ilimler hocasıydı. İyi eğitim almıştı, ama hakikaten yaratıcı olduğu pek bir eseri yoktu. Bu 47. maddeye öylesine hayran kaldı ki, ispatını anlayabilmek için sabırla kitabın tamamını okudu. Ve ispattaki sade ve tutarlı akıl yürütmenin beşeri ilimlere uygulanması gerektiğine karar verdi. Bunu yapmaya çalıştı ve şimdi kendisini siyaset bilimi ve felsefesinin gelmiş geçmiş en büyük isimlerinden birisi olarak görüyoruz. Bilin bakalım bir insanın dünyaya bakışını ve tüm dünya siyasetini değiştiren bu 47. madde neydi?

Bu örneklere rağmen, hâlâ ikna olmadıysanız fizikteki, matematikteki güzelliği bir az düzgün eğitimden sonra hepimizin görebileceğine, sizi bir de yapay zeka uzmanı Jürgen Schmidhuber’i dinlemeye davet edebilirim. Schmidhuber’ın “Eğlence ve Yaratıcılığın Örgün Kuramı” diye adlandırdığı ilginç bir kuramı var. Güzelliği bir sistemdeki toplam enformatik bilgi miktarının ne kadar sıkıştırılabileceğinin ölçüsü olarak tanımlıyor. Bizi heyecanlandıran ise beynimizin daha önceden fark etmediğimiz yeni bir sıkıştırma algoritması öğrenmesi ile veriyi daha az sayı ile ifade edebilmesi. Bu açıdan yaklaşınca güzel bir yüze baktığınızda beynimizin yaptığı iş ile, bir fizikçinin evrenin sırlarını açıklayan matematiksel kanunlar keşfetmesi veya bir müzisyenin yeni bir melodi yaratması aslında tek bir potada eriyen birbirine paralel faaliyetler. Yani biraz abartırsak diyebiliriz ki, eğer güzellik yarışması izleyebiliyorsak, veya Pele’nin futbolundaki güzelliği görebiliyorsak, veya Cem Yılmaz esprilerine gülebiliyorsak, doğru yaklaşımla pek âlâ matematik ve fizikteki eşsiz güzelliği de yakalayabilir beynimiz.

Schmidhuber'ın 1998’deki bir makalesi için hazırladığı ve matematiksel oranlar ile ortaya çıkartılan bilgisayarda oluşturulmuş bir insan yüzü. Da Vinci veya Dürer gibi sanatçılar da eserlerinde benzeri şekilde oranlar kullanıyorlardı.   

Müzik dersine muhalefetim sebebiyle müziksiz bir hayata kendimi mahkum etmedim. Müzisyen değilim (çok isterdim), ama müzik hakikaten ruhumun gıdası. Siz de eğer fizik ve matematik derslerinde mutsuz olduysanız, bunun sizi fiziksiz ve matematiksiz bir hayata mahkum etmesine izin vermeyin. Fizikçi veya matematikçi olmak gerekmiyor, bu dalların insana kendisi ve evrenle ilgili söylediklerini duyabilmek için. Bu mesleklerde güzellik öylesine önemli bir kriter ki, tonlarca fizikçi için denklemlerdeki güzellik kuramsal fiziğin vazgeçilmez parçasıdır. Bunları öğrenmek bel ağrılarınıza deva olamayabilir ama görünmez güzellikleri sizin için görünür kılabilir, adeta kesilmemiş bir taşın işlendikten sonra güzellik sembolü bir elmasa dönüşmesi gibi.

Kaynaklar
SES Dergisi - Sanayi Eczacılarının Sesi/ Jogo Bonito Yazısı
http://issuu.com/isteo/docs/ses_6_dergi_web/1?e=6654171/30143176

¹Queen’den Innuendo.
²Semir Zeki ve diğerleri, The experience of mathematical beauty and its neural correlates, Frontiers in Human Neuroscience, 8 (2014) 1. doi: 10.3389/fnhum.2014.00068
³Futbola “güzel oyun” diye isim takan kişi Pele değil, ancak bu terim özellikle onunla beraber anılıyor; otobiyografisinin başlığı Hayatım ve Güzel Oyun olduğu için sanırım.
⁴Elisha Scott Loomis, The Pythagorean Proposition, 1940.
⁵Öyle ki, Hobbes toplumsal sözleşme kuramının başlangıcı kabul edilen Leviathan kitabının dördüncü kısmında geometriyi Tanrı’nın insana armağan ettiği yegane gerçek bilim diye tanımlayacaktır. 
⁶Youtube’da çok keyifli ve espirili konuşmaları mevcut.
⁷Örneğin 1933 Nobel Fizik Ödülü’nün sahibi Paul Dirac’a göre güzellik ve içgüdü doğru yolda olduğunuzun habercisidir.
⁸Bu örneği vermeden güzellikle ilgili bir yazıyı bitirmeye gönlüm el vermedi. Eğer ham elmas gördüyseniz, hiç de öyle göz kamaştırıcı bir taş olmadığını bilirsiniz. Onu pırlanta haline getiren ise fiziktir. Günümüzde standart pırlanta kesim tekniği (özellikle A.B.D.’de) Tolkowsky kesimi diye bilinir. 1919’da Marcel Tolkowsky’nin ışığın kırılması ve yansımasıyla ilgili formülleri kullanarak elmasın kendi üzerine düşen ışığı geri yansıtabilmesi ve gök kuşağındaki tüm renkleri ortaya çıkarabilmesini sağlayan geometrik oranları hesaplaması sayesinde pırlantalar gül kesimli elmaslardan daha parlak olmuş ve yüzüklerdeki yerlerini almışlardır.